基于神经网络中卷积操作的标量声波方程正演模拟
编写一个声波方程的正演模拟程序,是入门地震数据处理中数值模拟这一领域的基础,同时也是后续做RTM、FWI等方向的基础。个人一般用C、C++ 或者CUDA编写CPU(GPU) 版本的程序,对于初入这一行业的小白来讲门槛比较高,既要掌握语言语法、还要将偏微分方程“变现”(将其离散化并变为计算机语言),并且后续代码的移植也非常困难;但好处是可操作性强(可以直接对内存、显存进行操作),代码可读性强(不会像python一样过一阵再看自己写的代码就看不懂了)。
所以… … …
之前做过一些尝试,把C的正演程序直接改成python的语法,但是发现效率极其低下,已经找不到当时的代码了,回忆了一下应该是思维定式(菜)惹的祸:波场计算的时候用for循环处理了numpy数组(大误),现在想想是真的菜。
下面我们以深度学习中卷积操作的视角重新审视一下基于有限差分的标量声波方程正演模拟。
标量声波方程
我们首先来看二维空间中的波动方程,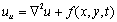
左侧是u对时间的二阶导数,右侧是u对空间的二阶偏导数与源f之和,为求解 t时刻 (i, j) 处的波场分量,首先需要将其离散化。我们一般将二维空间中的拉普拉斯算子用Taylor展开的形式来逼近,用k、k-1、和k-2表示相邻的三个时刻,空间步长dx=dz=dh,时间步长为dt,介质速度为Vp,则有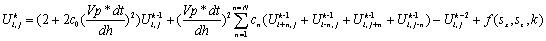
我们会发现它实质上是一个迭代的过程,这里给出的公式只能够计算一个时间切片内的波场,在编程计算时,计算完k时刻波场后,需要将k和k-1时刻分别更新为k-1和k-2时刻,这样就可以计算下一个”k”时刻的波场(对应实际的k+1)。
神经网络中的卷积操作
神经网络中的二维卷积实质上是卷积核与像素矩阵pixel-wise的互相关、求和,它与一维信号中的卷积还不太一样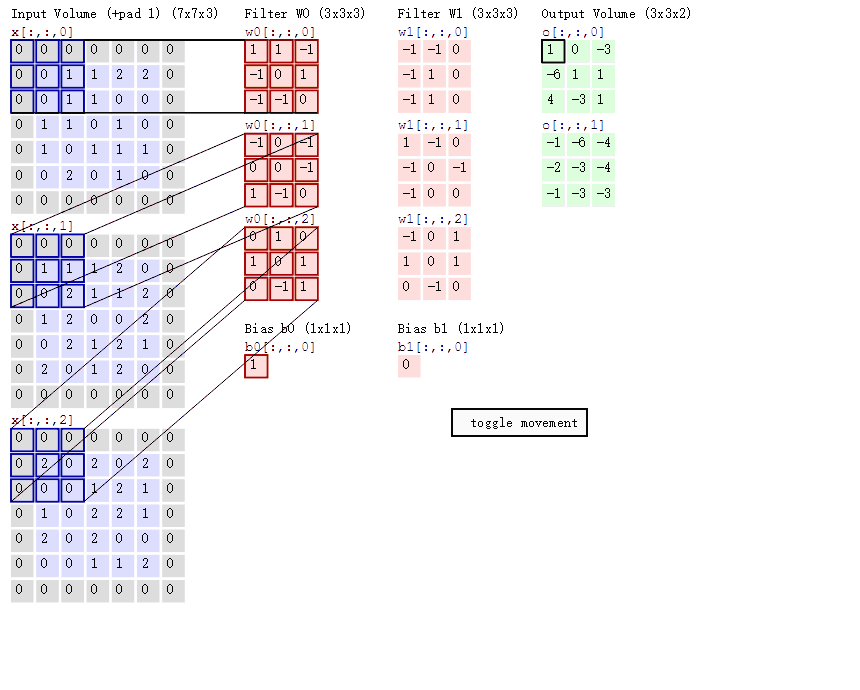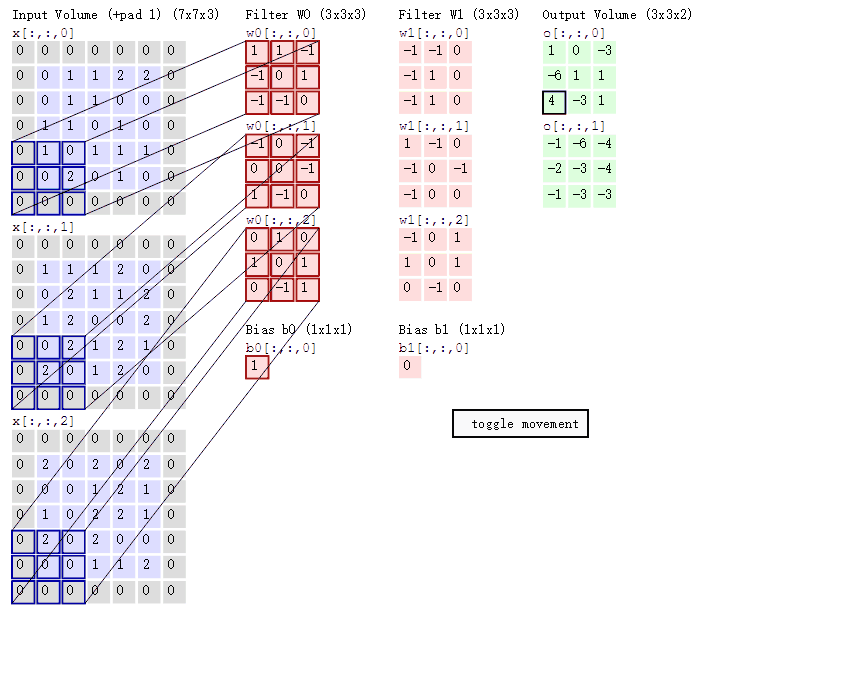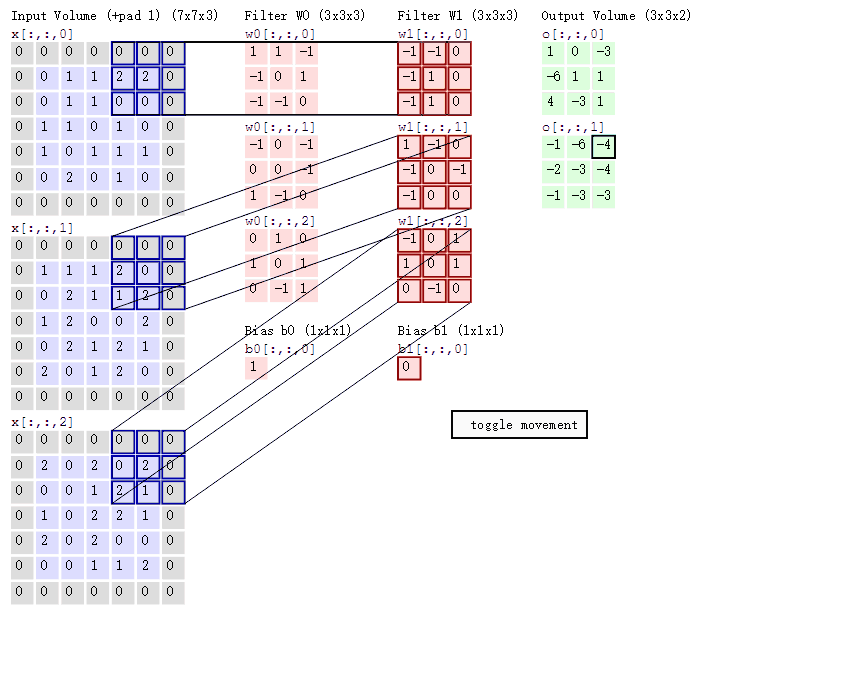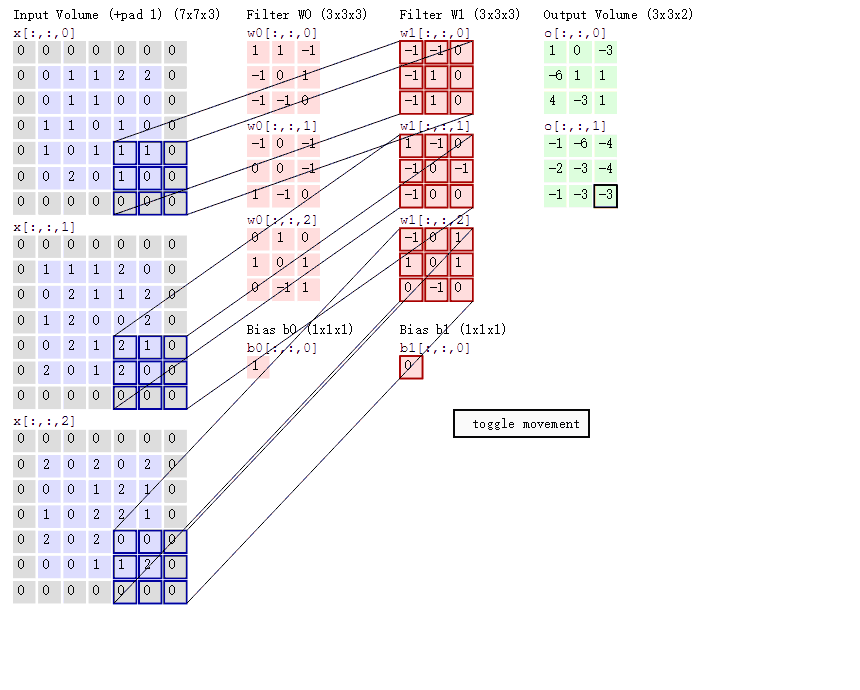
图片来自(简书)
动图中可以很明显地看出,单层的卷积计算也并不是很复杂,只是拿一个window在已知的输入上滑动,这个window就是神经网络卷积、反卷积中的卷积核kernel,滑动的步长被称为stride,边缘处灰色值被称为padding(用于填充边缘保证输入和输出的大小),kernel和输入的每一个block相乘相加即可得到输出的一个像素值。
基于卷积op的有限差分
很久之前就在想有没有办法能够将正演接入神经网络中,利用python中现成的工具包快速完成一些复杂的计算,这要涉及到数据流问题、输入输出转换问题、数据接口问题等等。前一阵利用pycuda完成了几个版本的正演模拟(常规网格标量声波和一阶速度应力交错网格弹性波)计算package,能够通过简单的输入速度模型(numpy)和参数设置生成数据流并怼到神经网络里面,但是pycuda的底层代码还是用CUDA写的,只是通过它的SourceMoudle来编译运行,所以不能直接接到TF的Graph中,进行更加高级的运算,比如求导等(package中有未公开发表的部分,待发表后将源码放出)。
要想利用TF等框架的自动微分,就必须要使用TF原生的函数或者定义 @tf.function来追踪变量,由此有了以下尝试。
我们观察离散格式的标量声波方程中带有求和符号的一项,可以看到它是每一个点上沿着x方向和z方向的求和叠加,假设有限差分精度为2N,那么求和项中的系数可以通过求解以下方程得到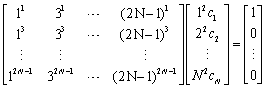
仔细观察即可发现,每个(i,j)处横向或纵向的求和都可以用以该点为中心,长度和宽度均为2*N+1的block与一个相同大小的卷积核f进行卷积来代替,例如当差分精度为4时,卷积核的大小应为5x5,以(i,j)为中心的求和(dx=dz=dh)可以用如下卷积操作代替(注:第一个矩阵中的省略号不代表值为0,只是其与卷积核相乘后的值为0,当网格不同方向的大小不同时需要区分水平方向卷积核以及垂直方向卷积核),那么整个卷积就可以写为tf.nn.depthwise_conv2d(input=x, filter=f, strides=[1, 1, 1, 1], padding='SAME')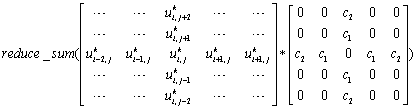
基本原理如上所述,这样一来,我们就可以利用TF框架来实现正演模拟了(完整的代码请联系shaowinw@geophyai.com,小站流量不多了,暂不提供下载功能)。