GeophyAI

Python与地球物理数据处理

0%

Wave physics as an analog recurrent neural network

发表于 分类于 Valine：
《Wave physics as an analog recurrent neural network》一文翻译

Wave physics as an analog recurrent neural network

原文地址：模拟递归神经网络的波动物理
doi: 10.1126/sciadv.aay6946
翻译时间：2021年4月23日

ABSTRACTS

模拟机器学习硬件平台有望比数字平台更快、更节能。声学和光学中的波物理，是为时变信号构建模拟处理器最自然的选择。本文明确了波动物理与RNN（Recurrent neural networks，循环神经网络）之间的映射。这种映射表明，利用标准的神经网络训练技术，可以使物理波动系统学习到时序数据中的复杂特征。例如，我们证明了，当原始音频信号在逆向设计的非均匀介质中散射和传播时，能够实现元音分类（vowel classification），且其性能与RNN的“数字化实现”相当。这些发现为一类新的模拟机器学习平台提供了可能，该平台能够快速有效地对数据在其原有域进行处理（即不通过将问题转化网络训练的方式）。

INTRODUCTION

近年来，机器学习在执行复杂的信息处理任务方面取得了巨大的成功，例如计算机视觉（CV)[1]、机器翻译[2]等传统上难以处理的领域。然而，
这些应用的计算需求正呈指数级增长，促使人们不断开发新的、专门的硬件平台，以便快速高效地执行机器学习模型，其中包括从架构上模仿大脑生物电路的神经形态硬件平台[3][4][5]等。此外，使用连续物理系统自然演化来执行计算的模拟计算平台也正在成为实现机器学习的一个重要方向[6][7][8][9][10]。本项工作中，我们发现了诸如声波、光学等波动物理现象与RNN计算之间的映射关系。RNN是最重要的机器学习模型之一，其已被广泛用于执行自然语言处理[11]和时间序列预测[12][13][14]等任务。我们证明了基于波的物理系统可以训练成RNN，因此，可以被动地处理数据原有域的信号和信息，而无需进行模数转换，从而有效提升处理效率并降低功耗。在这个框架中，与有意将信号反馈给输入不同的是，递归关系自然地发生在物理本身的时间动力学中，用于信息处理的内存和容量由在空间中传播的波提供。

RESULTS

波动力学与RNN之间的等效性

本节中，我们介绍RNN运算与波动力学之间的关系。RNN通过对输入序列逐步应用相同的基本运算来得到输出序列，先前时刻的信息则被编码到RNN的隐藏状态中并在每个时刻进行更新。隐藏状态允许RNN保存历史信息的记忆，并学习到数据的时间结构以及长程依赖关系[15][16]。在给定的时刻$\boldsymbol t$，RNN作用于输入矢量$\boldsymbol x_t$以及隐藏状态矢量$\boldsymbol h_{t-1}$，计算得到输出矢量$\boldsymbol y_t$以及更新后的隐藏状态$\boldsymbol h_t$。
RNN有多种表现形式，其中最常见的形式其更新公式如下所示：

如图1B所示。稠密矩阵$\boldsymbol W^{(h)}$、$\boldsymbol W^{(x)}$、$\boldsymbol W^{(y)}$是训练过程中不断优化得到的，$\sigma^{(h)}(·)$和$\sigma^{(y)}(·)$为非线性激活函数。当公式1、2所定义的运算作用于输入序列时，有向图如1C所示。
接下来我们讨论如式1、2所示的RNN与波动物理系统之间的关系。举个例子，标量波场分布$\boldsymbol u(x, y, z)$由二阶偏微分方程$3$（图1D）控制。

其中，$\nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}$为拉普拉斯算子，$c=c(x, y, z)$为波速的空间分布，$f=f(x, y, z, t)$为源项。公式3的递推离散形式（以$\Delta t$为时间步长）为：

其中，下标$t$表示在固定时刻的标量场值。波动系统的隐藏状态-Hidden stae被定义为当前时刻和前一时刻波场分布的级联(concatenation)，$\boldsymbol h_t \equiv[\boldsymbol u_{t-1}, \boldsymbol u_{t-1}]^T$，其中$\boldsymbol u_t$和$\boldsymbol u_{t-1}$均为定义在离散空间网格上的标量场$u_t$和$u_{t-1}$拉平(flatten)后的矢量。此时，波动方程的更新公式可改写为

其中稀疏矩阵$A$，描述了无源波场$\boldsymbol u_t$和$\boldsymbol u_{t-1}$的更新量（如图1E所示）。公式$5$和$6$推导过程见S1。
对于足够大的场强，$A$对$\boldsymbol h_{t-1}$的依赖性可以通过形式为$c=c_lin+u^{2}_t·c_{nl}$的强度依赖波速实现，其中$c_{nl}$表现为介质局部区域中的非线性响应。事实上，这种类型的非线性响应会在各种博物理线性中遇到，例如水波、Kerr效应[19]的非线性光学材料、起泡流体以及柔软介质中的声波[20]等。章节S2中提供了非线性材料响应的讨论和分析。正如激活函数$\sigma^{(y)}(·)$之于标准RNN中，当输出为波强度度量时，隐藏状态$\boldsymbol h_t$和输出$\boldsymbol y_t$之间的非线性关系在波动物理中也是非常典型的，正如公式$6$所示。
与标准RNN类似，波动方程中隐藏状态以及输入和输出之间的关系是由线性算子定义的，这里给定$\boldsymbol P^{(i)}$和$\boldsymbol P^{(o)}$。这些矩阵给定了空间中的注入(injecting)和测量(measuring)点。与输入和输出均为密集矩阵的标准RNN不同的是，波动方程的输入和输出矩阵都是稀疏的，因为他们只在注入和测量点是非零的。此外，这些矩阵在训练过程中都是不变的。与矩阵构造相关的更多信息请参照章节S3。
波动方程中可训练的自由参数为波速$c(x, y, z)$，对应于实际中材料的物理配置和布局。因此，当以离散时间（图1E）进行建模时，波动方程定义了一个映射到RNN的运算（图1B）。与RNN相类似，整个波动方程的动态过程可以被视为一个有向图，但相反的是，拉普拉斯算子的存在（最近邻耦合）使得信息通过隐藏层的速度是有限的。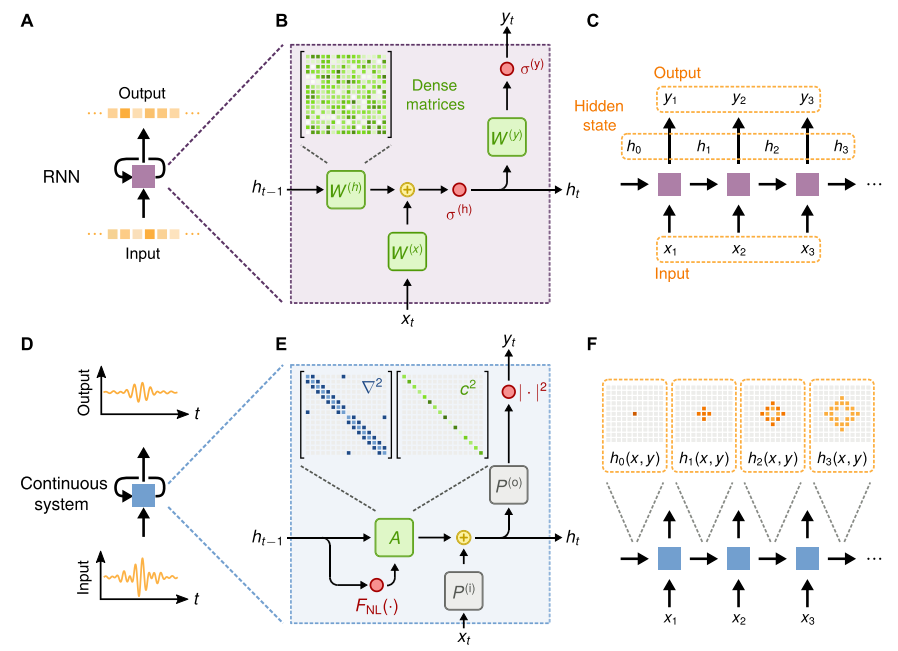
RNN
图1.标准RNN和基于波动物理系统的概念比较(A)作用于离散输入序列上并产生离散输出序列的RNN单元图(B)RNN单元的内部组成部分，由可训练密集矩阵$\boldsymbol W^{(h)}$、$\boldsymbol W^{(x)}$、$\boldsymbol W^{(y)}$组成。隐态和输出的激活函数分别用$\sigma^{(h)}$和$\sigma^{(y)}$表示(C)RNN单元的有向图(D)连续物理系统在连续输入序列上运行并产生连续输出序列的循环表示图(E)波动方程用有限差分离散时递推关系的内部分量(F)连续物理系统离散时间步长的有向图，以及波扰动如何在空间内传播示意图。

DISCUSSION

本文提出的基于波动力学的RNN具有许多优点，为其处理时间编码信息提供了可能。与标准RNN不同的是，波动方程从一个时刻到下一个时刻的更新通过拉普拉斯算子（由图1E中的稀疏矩阵表示）强制隐态元素之间的最近邻耦合。这种近邻耦合是由于波动方程是一个双曲偏微分方程，其中信息以有限的速度传播。因此，模拟RNN隐藏状态的大小，以及它的存储容量，直接由传播介质的大小决定。此外，与传统的RNN不同，波动方程加强了能量守恒约束，防止了隐态范数和输出信号的无限增长。相反，定义标准RNN更新关系的无约束稠密矩阵将会导致梯度消失和爆炸，这对传统RNN的训练提出了重大挑战[27]。

我们已经证明了波动方程动力学在概念上等同于RNN。这种概念上的联系为一类新的模拟硬件平台提供了机会，在这种平台中，演化的时间动力学在物理和数据集中都扮演着重要角色。虽然我们把重点放在最一般的例子波动动力学（标量波动方程），我们的结果可以很容易地扩展到其他类波物理。这种利用物理进行计算的方法[9][28][32]可能会为模拟机器学习设备提供一个新的平台，它有可能比数字设备更自然、更有效地进行计算。该方法的普遍性进一步表明，许多物理系统可能是对动态信号（例如光学、声学或地震学中的信号）执行类似RNN的计算。

MATERIALS AND METHODS

Numerical modeling

利用Python编写的自定义软件包对波动方程物理进行了数值模拟和仿真。该软件是在流行的机器学习库PyTorch[33]的基础上开发的，通过逆向模式自动微分计算损失函数相对于材料分布的梯度。在物理和工程领域的逆设计中，这种梯度计算方法通常被称为伴随变量法，并且需要额外进行一次模拟。我们注意到，在地震数据集的全波形反演中，已经提出了使用机器学习框架进行数值模拟的相关方法[34]。进行数值模拟和波动方程训练的代码，以及生成本文中给出的图形的代码，可在github上找到。

参考文献

  1. 1.O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, L. Fei-Fei, Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 115, 211–252 (2015). ↩
  2. 2.I. Sutskever, O. Vinyals, Q. V. Le, Sequence to sequence learning with neural networks, in Advances in Neural Information Processing Systems, NIPS Proceedings, Montreal, CA, 2014. ↩
  3. 3.J. M. Shainline, S. M. Buckley, R. P. Mirin, S. W. Nam, Superconducting optoelectronic circuits for neuromorphic computing. Phys. Rev. Appl. 7, 034013 (2017). ↩
  4. 4.A. N. Tait, T. F. D. Lima, E. Zhou, A. X. Wu, M. A. Nahmias, B. J. Shastri, P. R. Prucnal, Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 7, 7430 (2017). ↩
  5. 5.M. Romera, P. Talatchian, S. Tsunegi, F. Abreu Araujo, V. Cros, P. Bortolotti, J. Trastoy, K. Yakushiji, A. Fukushima, H. Kubota, S. Yuasa, M. Ernoult, D. Vodenicarevic, T. Hirtzlin, N. Locatelli, D. Querlioz, J. Grollier, Vowel recognition with four coupled spin-torque nano-oscillators. Nature 563, 230–234 (2018). ↩
  6. 6.Y. Shen, N. C. Harris, S. Skirlo, M. Prabhu, T. Baehr-Jones, M. Hochberg, X. Sun, S. Zhao, H. Larochelle, D. Englund, M. Soljačić, Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017). ↩
  7. 7.J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, S. Lloyd, Quantum machine learning. Nature 549, 195–202 (2017). ↩
  8. 8.F. Laporte, A. Katumba, J. Dambre, P. Bienstman, Numerical demonstration of neuromorphic computing with photonic crystal cavities. Opt. Express 26, 7955–7964 (2018). ↩
  9. 9.X. Lin, Y. Rivenson, N. T. Yardimci, M. Veli, Y. Luo, M. Jarrahi, A. Ozcan, All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018). ↩
  10. 10.E. Khoram, A. Chen, D. Liu, L. Ying, Q. Wang, M. Yuan, Z. Yu, Nanophotonic media for artificial neural inference. Photon. Res. 7, 823–827 (2019). ↩
  11. 11.K. Yao, G. Zweig, M.-Y. Hwang, Y. Shi, D. Yu, Recurrent neural networks for language understanding (Interspeech, 2013), pp. 2524–2528; https://www.microsoft.com/en-us/ research/publication/recurrent-neural-networks-for-language-understanding/. ↩
  12. 12.M. Hüsken, P. Stagge, Recurrent neural networks for time series classification. Neurocomputing 50, 223–235 (2003). ↩
  13. 13.G. Dorffner, Neural networks for time series processing. Neural Net. World 6, 447–468 (1996). ↩
  14. 14.J. T. Connor, R. D. Martin, L. E. Atlas, Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Netw. 5, 240–254 (1994). ↩
  15. 15.J. L. Elman, Finding structure in time. Cognit. Sci. 14, 179–211 (1990). ↩
  16. 16.M. I. Jordan, Serial order: A parallel distributed processing approach. Adv. Physcol. 121, 471–495 (1997). ↩
  17. 17.I. Goodfellow, Y. Bengio, A. Courville, Deep Learning (MIT Press, 2016). ↩
  18. 18.F. Ursell, The long-wave paradox in the theory of gravity waves. Math. Proc. Camb. Philos. Soc. 49, 685–694 (1953). ↩
  19. 19.R. W. Boyd, Nonlinear Optics (Academic Press, 2008). ↩
  20. 20.T. Rossing, Springer Handbook of Acoustics (Springer Science & Business Media, 2007). ↩
  21. 27.L. Jing, Y. Shen, T. Dubcek, J. Peurifoy, S. Skirlo, Y. LeCun, M. Tegmark, M. Soljačić, Tunable Efficient Unitary Neural Networks (EUNN) and their application to RNNs, Proceedings of the 34th International Conference on Machine Learning-Volume 70 (JMLR.org, 2017), pp. 1733–1741. ↩
  22. 28.A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alù, N. Engheta, Performing mathematical operations with metamaterials. Science 343, 160–163 (2014). ↩
  23. 32.N. M. Estakhri, B. Edwards, N. Engheta, Inverse-designed metastructures that solve equations. Science 363, 1333–1338 (2019). ↩
  24. 33.A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga, A. Lerer, Automatic differentiation in PyTorch, Workshop on Autodiff (NIPS, 2017). ↩
  25. 34.A. Richardson, Seismic full-waveform inversion using deep learning tools and techniques. arXiv:1801.07232 [physics.geo-ph] (22 January 2018). ↩