原文地址:PINN:深度学习框架下求解含有非线性偏微分方程的正问题、反问题
doi:10.1016/j.jcp.2018.10.045
ABSTRACT
本文介绍了PINN(Physics-informed neural networks,物理信息神经网络),其能够在解决监督学习任务的同时遵守由一般的非线性偏微分方程描述的物理约束。在这项工作中,我们主要从数据驱动解和偏微分方程的数据驱动解两方面探讨。根据可用数据的性质和排列(nature and arrangement),我们设计了两种不同类型的算法,即连续时间模型和离散时间模型。第一类模型形成了一族数据高效(data-efficient)的时空函数逼近器(spatio-temporal function approximators),而后一类模型能以任意精度的隐式Runge-Kutta时间递推格式(with unlimited number of stages)。通过流体、量子力学、反应扩散系统和非线性浅水波的传播等一系列经典问题,证明了该框架的有效性。
Introduction
随着可用数据量和计算资源的爆炸式增长,机器学习与数据挖掘的最新成果在不同领域的应用产生了变革性影响,流入图像识别[1]、认知科学[2]、基因组学[3]等。然而,在分析复杂的物理、生物或工程系统的过程中,数据采集的成本往往过高,有时我们不得不使用有限的信息作出决策。在这种小数据环境下,绝大多数最先进的机器学习技术(如深度/卷积/递归神经网络)缺乏鲁棒性,无法保证收敛性。
乍一看,训练一个神经网络,使其能够从几个可能是高维的输入和输出中学习到非线性映射是非常幼稚的。在许多物理和生物系统建模相关的案例中,往往存在有大量的先验知识,而这些知识还没有应用于现有的机器学习中。假设它是控制系统随时间变化的动力学物理定律,或一些已经经过经验验证的规则或其他领域的专业知识,这些先验信息可以作为正则化约束,将解限制在可以接受的范围内(例如,在不可压缩流体中,舍弃任何违背质量守恒定律的不现实的流动解)。将这种结构化信息编码为学习算法会放大算法所看到的数据中的信息含量,使其能够快速地向正确方向收敛,并且即使只有少数训练数据也能获得较好的泛化性。
近期许多研究[4][5][6]已经展示了如何利用结构化先验信息构建数据高效和物理可靠(physical-informed)的模型。这里,我们利用高斯过程回归(Gaussian Process Regression)[7]设计了一个适合于给定线性算子的函数表示,其能够准确推断解并为多个数学物理问题提供不精确的解。在推理和系统辨识的背景下,Raissi 等人[8][9]在后续研究中提出了非线性问题的推广。尽管高斯过程在编码先验信息时具有灵活性和数学优雅性,但其对非线性问题的处理有两个重要的限制。首先,在[8][9]中,作者必须在时间上对任何非线性项进行局部线性化,从而限制了所提出方法在离散时域的适用性,并损害了它们在强非线性状态下预测的准确性。其次,高斯过程回归的贝叶斯性质有一定的先验假设,这些假设可能限制模型的表达能力,并产生鲁棒性/脆性(robustness/brittleness)问题,特别是对于非线性问题的处理[10]。
Problem setup
在这项工作中,我们采取了一种不同的方法:利用深度神经网络和它们众所周知的作为普适函数逼近器的能力[11]。在这种情况下,我们可以直接处理非线性问题,而无需任何先验假设,线性化,或局部时间递推。我们利用自动微分技术的最新发展[12]——这是科学计算中最有用但可能利用不足的技术之一——根据输入坐标和模型参数对神经网络进行微分,以获得物理可靠的神经网络。这类神经网络被约束为遵守任何对称性、不变性或守恒原理,这些原理源于控制观测数据的物理定律,如一般的时间相关和非线性偏微分方程所模拟的那样。这种简单而强大的结构使我们能够解决计算科学中的一大类问题,并引入了一种潜在的变革性技术,从而开发出新的数据高效和物理可靠的学习机,新的偏微分方程数值解算器,以及用于模型反演和系统辨识的数据驱动方法。
为此,我们的手稿分为两部分,旨在介绍我们在两大类问题背景下的发展:数据驱动的偏微分方程解和数据驱动的偏微分方程求解。论文相关的代码和数据集地址Github。在这项工作中,我们只使用了相对简单的深度前馈神经网络结构,其具有双曲正切激活函数,并且没有额外的正则化(例如,L1/L2惩罚、Dropout等)。手稿中的每个数值例子都附有关于我们所采用的神经网络结构的详细讨论,以及关于其训练过程的详细信息(例如优化器、学习率等)。最后,附录A和附录B中提供了一系列全面的系统研究,旨在证明所提出方法的性能。
在这项工作中,我们考虑一般形式的参数化和非线性偏微分方程
其中,$u(t, x)$表示隐式解(latent, hidden),$\mathcal{N}[·;\lambda]$为以$\lambda$为参数的非线性算子,$\Omega$为$\R^N$的子集。上述公式表示了数学物理中的一系列问题,包括守恒定律、扩散过程、平流-扩散-反应系统以及动力学方程等。本文以一维空间中的Burgers方程[13]为例,其中$\mathcal{N}[u;\lambda]=\lambda_1uu_x-\lambda_2u_{xx}$、$\lambda=(\lambda_1,\lambda_2)$,下标表示对时间或空间的偏微分。考虑到系统的噪声测量,我们对以下两种情况下的解感兴趣:
1.给定模型参数$\lambda$,怎样描述系统的隐态$u(t, x)$;此类问题涉及到推理、滤波、平滑或者数据驱动的偏微分方程求解[4][8]
- 模型参数$\lambda$为何值时能够最好地描述观测数据;第二类问题涉及到学习、系统识别、数据驱动的偏微分方程反问题[5][9][14]。
3 Data-driven solutions of partial differential equations
首先我们来看如何利用数据驱动的方式计算偏微分方程的解:其中,$u(t, x)$表示隐式解(latent, hidden),$\mathcal{N}[·;\lambda]$为以$\lambda$为参数的非线性算子,$\Omega$为$\R^N$的子集。在如下章节中,我们提出了两种不同的算法,分别命名连续时间模型和离散时间模型。分别通过不同的基准问题来突出它们的特性和性能。在我们研究的第二部分(下一节),我们将注意力转移到偏微分方程的数据驱动发现问题上[5][9][14]。3.1 连续时间模型
我们定义$f(t, x)$由方程$2$左侧给出,即然后用神经网络逼近$u(t, x)$。这个假设和方程$3$共同构成了一个PINN $f(t, x)$。该网络可通过链式求导法则[12],并且与网络表示$u(t, x)$具有相同的参数,尽管由于微分算子$N$的作用而具有不同的激活函数。神经网络$u(t, x)$和$f(t, x)$之间的共享参数可通过最小化均方误差(MSE)函数来学习。其中这里,$\lbrace t_{u}^{i}, x_{u}^{i}, u^{i} \rbrace$表示$u(t, x)$的初始和边界训练数据,$\lbrace t_{f}^{i}, x_{f}^{i}\rbrace$表示$f(t, x)$的collocations points。损失函数$MSE_u$对应初始和边界数据,$MSE_f$在配置点的有限集合上加强了方程$2$所施加的结构(????)。尽管在以前的研究[15][16]中已经探讨了使用物理定律约束神经网络的类似想法,但在这里我们使用现代计算工具重新讨论了它们,并将它们应用于与时间相关的非线性偏微分方程描述等更具挑战性的动力学问题中。
在这里,我们强调这一工作与文献中现有的机器学习在计算物理中的应用之间的重要区别。Wang等人[17]最近在湍流建模的背景下也使用了术语“物理信息机器学习”。[18][19][20][21][22][23][24][25][26][27][28][29]等也使用了物理系统预测建模的机器学习方法。所有这些方法都使用机器学习算法,例如支持向量机、随机森林、高斯过程和前馈/卷积/递归神经网络,仅仅将这些算法作为“黑盒子”来使用,即只建立了模型但模型所代表的的物理含义不明。如上所述,本文工作旨在更进一步,为基础微分算子重新构造“定制”激活函数和“定制”损失函数。这使我们能够在理解和欣赏自动微分在深度学习领域中所起的关键作用的同时打开机器学习的黑匣子。一般来说,自动微分,特别是反向传播算法,是目前训练深度模型的主要方法,其通过对模型的参数(如权重和偏差)求导。在这里,我们与使用深度学习中完全相同的自动微分技术求取PINN相对于输入空间坐标和时间的导数,其中的物理过程由偏微分方程所描述。我们观察到,这种结构化方法引入了一种正则化机制,允许我们使用相对简单的前馈神经网络结构,并用少量数据对其进行训练。这个简单想法的有效性可能与Lin、Tegmark和Rolnick[30]提出的评论有关,并提出了许多有趣的问题,有待在未来的研究中定量解决。感谢[15][16][31][32][33][34]等人为本文所提供的灵感。
在所有数据驱动求解偏微分方程的例子中,训练数据$N_u$的总数
相对较小(几百点到几千点),我们选择使用L-BFGS优化所有损失函数,L-BFGS是一种基于拟牛顿、全批次梯度的优化算法[35]。对于更大的数据集,如下一章节中讨论的数据驱动模型,可以使用随机梯度下降及其变种等计算效率更高的小批量优化算法[36][37]。尽管理论上不能保证这个过程收敛到一个全局极小值,但我们的经验证据表明,如果给定的偏微分方程是适定的且其解是唯一的,在神经网络结构表达能力充分且有足够数量的配置点$N_f$的前提下我们的方法能够达到良好的预测精度。这一观察结果与方程$4$的均方误差损失所导致的优化景观密切相关,并定义了一个与深度学习的最新理论发展同步的研究开放问题[38][39]。为此,我们将使用本文提供的一系列系统敏感性研究来测试所提出方法的稳健性(见附录A和B)。3.1.1 例子(Schrodinger equation)
这个例子旨在强调我们的方法在处理周期性边界条件、复值解以及控制不同类型非线性偏微分方程中的能力。一维非线性薛定谔方程是研究量子力学系统的经典方程,包括非线性波在光纤和/或波导中的传播、玻色-爱因斯坦凝聚和等离子体波。在光学中,非线性项来源于给定材料的强度相关折射率效应。类似地,玻色-爱因斯坦凝聚的非线性项是N体系统的平均场相互作用的结果。非线性薛定谔方程和周期性边界条件由下式给出其中$h(t, x)$为复值解。我们定义$f(t, x)$由下式给出然后在$h(t, x)$之前设置一个复值神经网络。事实上,如果将$u$和$v$分别表示$h$的实部和虚部,相当于建立了一个多输出神经网络$h(t, x)=[u(t, x) v(t, x)]$,这就形成了复值多输出PINN-$f(t, x)$。$h(t, x)$和$f(t, x)$的共享参数可以通过最小化如下目标函数来优化得到这里,$\lbrace x^i_0, h^i_0\rbrace_{i=1}^{N_0}$表示初始值,$\lbrace t_b^i \rbrace_{i=1}^{N_b}$表示边界上的collocation points,$\lbrace t_f^i, x_f^i \rbrace_{i=1}^{N_f}$表示$f(t, x)$上的collocation points。因此,$MSE_0$表示初始数据上的$loss$,$MSE_b$表示周期性边界条件,$MSE_f$为惩罚项,在collocation points上不满足薛定谔方程。
为了评估我们的方法的准确性,我们用传统的光谱方法模拟了方程$5$以创建高分辨率数据集。特别地,设初始状态$h(0,x)=2sech(x)$且假设周期性边界条件$h(t -5)=h(t, 5)$,$h_x(t, -5)=h_x(t, 5)$。使用Chebfun package[40]的pectral Fourier discretization with 256 modes和显式$Runge–Kutta$时间积分器以时间间隔$\Delta t=\pi/2·10^-6$对公式$5$积分到时间$t=\pi/2$。通过以上数据驱动设置,我们记录latent function $h(t,x)$在$t=0$时的测量值$\lbrace x^i_0, h^i_0 \rbrace_{i=1}^{N_0}$。特别地,训练集包含从高分辨率数据集中随机选取的$N_0=50$个数据点,以及$N_b=50$ 个配置点$\lbrace t^i_b \rbrace^{N_b}_{i=1}$以确保满足周期边界条件。此外,我们还假设$N_f=20,000$个随机采样配置点以确保方程$5$在解空间内。所有随机采样点的空间位置均通过空间填充Latin Hypercude 采样策略获得[41]。
我们的最终目标是推断薛定谔方程$5$在整个时空域的解$h(t, x)$。我们选择使用深度为5、每层包含100个神经元以及激活函数为双曲正切的神经网络来表示latent function$h(t, x) = [u(t, x) v(t,x)]$。一般来说,神经网络应该具有足够的近似能力以满足$u(t, x)$的复杂性。尽管可以采用更系统的处理流程,如贝叶斯优化[42],以微调神经网络的设计,但在缺乏理论误差/收敛估计的情况下,神经结构/训练过程和基本微分方程的复杂性之间的相互作用仍然不清楚。评估预测解的准确性的一个可行途径是采用贝叶斯方法并监测预测后验分布的方差,但这超出了目前工作的范围,这是今后的研究方向。
在这个例子中,我们的设置旨在强调所提出方法相对于过拟合问题的鲁棒性。具体来讲,公式$6$中的$MSE_f$这一项起到了正则化的作用,它对不满足方程$5$的解起到惩罚的作用。因此,在物理系统中经常遇到数据采集成本非常高的情况,而PINN可以采用小样本容量的数据集进行训练。图1总结了我们的实验结果。特别的,图1上图展示了预测的时空解$\mid h(t, x) \mid=\sqrt{u^2({t, x})+v^2({t, x})}$的幅值,以及初始和边界训练数据的位置。使用测试数据获得预测误差,实测$L_2$误差为$1.97·10^{-3}$。预测解的更详细评估如图1的底部图例所示。特别地,我们在$t=0.59,0.79,0.98$的不同时刻对精确解和预测解进行了比较。基于物理信息的神经网络只需要少量的初始数据,就可以准确地捕捉薛定谔方程复杂的非线性特性。
到目前为止,连续时间神经网络模型的一个潜在局限性是,为了在整个时空域中实施物理信息约束,需要使用大量的配置点$N_f$。尽管在一维和二维情况中没有太大问题,但它可能会在高维问题中出现问题,因为全局执行物理约束(例如上述偏微分方程)所需的配置点总数将呈指数增长。尽管可以在一定程度上利用稀疏网格或准蒙特卡罗采样方案来解决这一限制[43][44],但在下一节中,我们提出了一种不同的方法,通过引入更结构化的神经网络表示,利用经典的$Runge-Kutta$时间递推方案来规避配置点的需要[45]。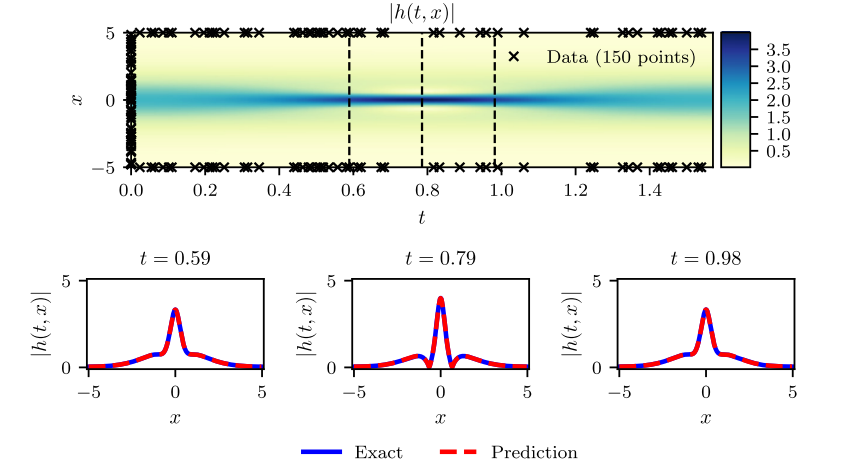
3.2 离散时间模型
对方程$2$应用$q$阶Runge-Kutta方法得到以下公式:
其中,$u^{n+c_j}(x)=u(t^n+c_j\Delta t, x)$($j=1,…,q$)。这一通用格式封装了显式和隐式时间递推格式,该格式取决于参数${a_ij, b_j, c_j}$。公式$7$可以被等价地表示为:
其中:
我们将多输出神经网络置于以下公式之前
上述先验信息以及公式$9$共同构成了以$x$为输入、以公式$11$为输出的PINN:
3.2.1 例子(Allen-Cahn方程)
这个例子旨在强调以上提出的离散时间模型处理不同类型非线性偏微分方程的能力。为此,让我们考虑Allen-Cahn和周期边界条件
Allen-Cahn方程是反散-扩散系统的著名方程。它描述了多组分合金体系的相分离过程,包括有序-无序转变。对于Allen-Cahn方程,公式$9$中的非线性算子为
公式$10$和$11$中的共享参数可通过最小化平方误差(公式$13$)学习来得到
其中,
$\lbrace x^{n, i}, u^{n, i}\rbrace _{i=1}^{N_n}$表示$t^n$时刻的数据。
在经典的数值分析中,受显式格式的稳定性约束或隐式公式的计算复杂性约束,时间步长通常被限制为较小值。随着Runge–Kutta阶数$q$增加,这些限制变得更加严格,并且对于大多数实际问题,需要进行数千到数百万个时间步长以达到最终时间。与经典方法形成鲜明对比的是,这里我们可以使用隐式Runge–Kutta格式,其中包含任意阶数,需要额外付出的成本非常小。这使得我们能够在保证稳定性和高预测精度的同时采取非常大的时间步长,所以允许我们仅通过一次递推就完成整个时空域求解。
在这个例子中,我们使用传统光谱法模拟$Allen-Cahn$方程得到了训练数据和测试数据。具体来讲,设初始条件为$u(0, x)=x^2cos(\pi x)$,周期性边界条件$u(t, -1)=u(t, 1)$和$u_x(t, -1)=u_x(t, 1)$,使用Chebfun包[40]以512modes的傅里叶光谱离散和四阶显式$Runge-Kutta$时间积分器($\Delta t=10^{-5}$)对公式$12$积分到$t=1.0$。
训练集包含$N_n=200$个从精确解中随机抽取的初始数据点,我们的目标是使用$\Delta t =0.8$的一次递推来预测$t=0.9$的解。为此,我们设计了一个包含4个隐藏层和每层200个神经元的PINN,输出则预测了101个感兴趣的数据,其中包含$q=100$的Runge-Kutta阶数$u^{n+c_i}(x), i=1,..,q$以及最终时刻的解$u^{n+1}_x$。该方案的理论误差估计预测了$O(\Delta t^{2q})$[45]的时间误差累积,在我们的例子中,其转化为低于机器精度的误差,即,$\Delta ^{2q}=0.8200≈ 10^{−20}$。据我们所知,这是第一次使用这种高阶隐式$Runge-Kutta$格式。值得注意的是,从$t=0.1$的光滑初始数据出发,我们可以在一个时间步长内预测t=0.9的近似不连续解,其相对$L_2$误差为$6.99·10−3$,如图2所示。这种误差完全归因于神经网络逼近$u(t, x)$的能力,以及误差平方和允许对训练数据进行插值的程度。
控制离散时间算法性能的关键参数是龙格库塔算法的阶数$q$和时间步长$\Delta t$。正如我们在附录A和附录B中提供的系统研究中所证明的,低阶方法,例如对应于经典梯形规则的情况$q=1$,以及对应于四阶$Gauss–Legendre$方法的情况$q=2$,不能保留它们对大时间步长的预测精度,因此,需要将其拆分成多个小时间步长。另一方面,将$Runge–Kutta$阶数设置为32个甚至更高,允许我们采取非常大的时间步长,并在不牺牲预测准确性的情况下使用一次地推有效地解决问题。此外,该方法能够充分保证数值稳定性,因为隐式$Gauss–Legendre$是唯一一类无论阶数如何都保持A-stable的时间递推格式,因此非常适合于刚性问题[45]。这些特性对于实现如此简单的算法来说是前所未有的,并且说明了我们离散时间方法的一个关键亮点。
参考文献
- 1.A. Krizhevsky, I. Sutskever, G.E. Hinton, Imagenet classifification with deep convolutional neural networks, in: Advances in Neural Information Processing Systems, 2012, pp. 1097–1105. ↩
- 2.B.M. Lake, R. Salakhutdinov, J.B. Tenenbaum, Human-level concept learning through probabilistic program induction, Science 350 (2015) 1332–1338. ↩
- 3.B. Alipanahi, A. Delong, M.T. Weirauch, B.J. Frey, Predicting the sequence specifificities of DNA- and RNA-binding proteins by deep learning, Nat. Biotechnol. 33 (2015) 831–838. ↩
- 4.M. Raissi, P. Perdikaris, G.E. Karniadakis, Inferring solutions of differential equations using noisy multi-fifidelity data, J. Comput. Phys. 335 (2017) 736–746. ↩
- 5.M. Raissi, P. Perdikaris, G.E. Karniadakis, Machine learning of linear differential equations using Gaussian processes, J. Comput. Phys. 348 (2017) 683–693. ↩
- 6.H. Owhadi, Bayesian numerical homogenization, Multiscale Model. Simul. 13 (2015) 812–828. ↩
- 7.C.E. Rasmussen, C.K. Williams, Gaussian Processes for Machine Learning, vol. 1, MIT Press, Cambridge, 2006. ↩
- 8.M. Raissi, P. Perdikaris, G.E. Karniadakis, Numerical Gaussian processes for time-dependent and non-linear partial differential equations, 2017, arXiv: 1703.10230. ↩
- 9.M. Raissi, G.E. Karniadakis, Hidden physics models: machine learning of nonlinear partial differential equations, 2017, arXiv:1708.00588. ↩
- 10.H. Owhadi, C. Scovel, T. Sullivan, et al., Brittleness of Bayesian inference under fifinite information in a continuous world, Electron. J. Stat. 9 (2015) 1–79. ↩
- 11.K. Hornik, M. Stinchcombe, H. White, Multilayer feedforward networks are universal approximators, Neural Netw. 2 (1989) 359–366. ↩
- 12.A.G. Baydin, B.A. Pearlmutter, A.A. Radul, J.M. Siskind, Automatic differentiation in machine learning: a survey, 2015, arXiv:1502.05767. ↩
- 13.C. Basdevant, M. Deville, P. Haldenwang, J. Lacroix, J. Ouazzani, R. Peyret, P. Orlandi, A. Patera, Spectral and fifinite difference solutions of the Burgers equation, Comput. Fluids 14 (1986) 23–41. ↩
- 14.S.H. Rudy, S.L. Brunton, J.L. Proctor, J.N. Kutz, Data-driven discovery of partial differential equations, Sci. Adv. 3 (2017). ↩
- 15.I.E. Lagaris, A. Likas, D.I. Fotiadis, Artifificial neural networks for solving ordinary and partial differential equations, IEEE Trans. Neural Netw. 9 (1998) 987–1000. ↩
- 16.D.C. Psichogios, L.H. Ungar, A hybrid neural network-fifirst principles approach to process modeling, AIChE J. 38 (1992) 1499–1511. ↩
- 17.J.-X. Wang, J. Wu, J. Ling, G. Iaccarino, H. Xiao, A comprehensive physics-informed machine learning framework for predictive turbulence modeling, 2017, arXiv:1701.07102. ↩
- 18.Y. Zhu, N. Zabaras, Bayesian deep convolutional encoder-decoder networks for surrogate modeling and uncertainty quantifification, 2018, arXiv:1801. 06879. ↩
- 19.T. Hagge, P. Stinis, E. Yeung, A.M. Tartakovsky, Solving differential equations with unknown constitutive relations as recurrent neural networks, 2017, arXiv:1710.02242. ↩
- 20.R. Tripathy, I. Bilionis, Deep UQ: learning deep neural network surrogate models for high dimensional uncertainty quantifification, 2018, arXiv:1802. 00850. ↩
- 21.P.R. Vlachas, W. Byeon, Z.Y. Wan, T.P. Sapsis, P. Koumoutsakos, Data-driven forecasting of high-dimensional chaotic systems with long-short term memory networks, 2018, arXiv:1802.07486. ↩
- 22.E.J. Parish, K. Duraisamy, A paradigm for data-driven predictive modeling using field inversion and machine learning, J. Comput. Phys. 305 (2016) 758–774. ↩
- 23.K. Duraisamy, Z.J. Zhang, A.P. Singh, New approaches in turbulence and transition modeling using data-driven techniques, in: 53rd AIAA Aerospace Sciences Meeting, 2018, p. 1284. ↩
- 24.J. Ling, A. Kurzawski, J. Templeton, Reynolds averaged turbulence modelling using deep neural networks with embedded invariance, J. Fluid Mech. 807 (2016) 155–166. ↩
- 25.Z.J. Zhang, K. Duraisamy, Machine learning methods for data-driven turbulence modeling, in: 22nd AIAA Computational Fluid Dynamics Conference, 2015, p. 2460. ↩
- 26.M. Milano, P. Koumoutsakos, Neural network modeling for near wall turbulent flow, J. Comput. Phys. 182 (2002) 1–26. ↩
- 27.P. Perdikaris, D. Venturi, G.E. Karniadakis, Multififidelity information fusion algorithms for high-dimensional systems and massive data sets, SIAM J. Sci. Comput. 38 (2016) B521–B538. ↩
- 28.R. Rico-Martinez, J. Anderson, I. Kevrekidis, Continuous-time nonlinear signal processing: a neural network based approach for gray box identification, in: Neural Networks for Signal Processing IV. Proceedings of the 1994 IEEE Workshop, IEEE, 1994, pp. 596–605. ↩
- 29.J. Ling, J. Templeton, Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty, Phys. Fluids 27 (2015) 085103. ↩
- 30.H.W. Lin, M. Tegmark, D. Rolnick, Why does deep and cheap learning work so well? J. Stat. Phys. 168 (2017) 1223–1247. ↩
- 31.R. Kondor, N-body networks: a covariant hierarchical neural network architecture for learning atomic potentials, 2018, arXiv:1803.01588. ↩
- 32.R. Kondor, S. Trivedi, On the generalization of equivariance and convolution in neural networks to the action of compact groups, 2018, arXiv:1802. 03690. ↩
- 33.M. Hirn, S. Mallat, N. Poilvert, Wavelet scattering regression of quantum chemical energies, Multiscale Model. Simul. 15 (2017) 827–863. ↩
- 34.S. Mallat, Understanding deep convolutional networks, Philos. Trans. R. Soc. A 374 (2016) 20150203. ↩
- 35.D.C. Liu, J. Nocedal, On the limited memory BFGS method for large scale optimization, Math. Program. 45 (1989) 503–528. ↩
- 36.I. Goodfellow, Y. Bengio, A. Courville, Deep Learning, MIT Press, 2016. ↩
- 37.D. Kingma, J. Ba, Adam: a method for stochastic optimization, 2014, arXiv:1412.6980. ↩
- 38.A. Choromanska, M. Henaff, M. Mathieu, G.B. Arous, Y. LeCun, The loss surfaces of multilayer networks, in: Artifificial Intelligence and Statistics, pp. 192–204. ↩
- 39.R. Shwartz-Ziv, N. Tishby, Opening the black box of deep neural networks via information, 2017, arXiv:1703.00810. ↩
- 40.T.A. Driscoll, N. Hale, L.N. Trefethen, Chebfun Guide, 2014. ↩
- 41.M. Stein, Large sample properties of simulations using Latin hypercube sampling, Technometrics 29 (1987) 143–151. ↩
- 42.J. Snoek, H. Larochelle, R.P. Adams, Practical bayesian optimization of machine learning algorithms, in: Advances in Neural Information Processing Systems, 2012, pp. 2951–2959. ↩
- 43.H.-J. Bungartz, M. Griebel, Sparse grids, Acta Numer. 13 (2004) 147–269. ↩
- 44.I.H. Sloan, H. Wo´zniakowski, When are quasi-Monte Carlo algorithms effiffifficient for high dimensional integrals? J. Complex. 14 (1998) 1–33. ↩
- 45.A. Iserles, A First Course in the Numerical Analysis of Differential Equations, vol. 44, Cambridge University Press, 2009. ↩
- 46.T. Von Kármán, Aerodynamics, vol. 9, McGraw-Hill, New York, 1963. ↩
- 47.G. Karniadakis, S. Sherwin, Spectral/hp Element Methods for Computational Fluid Dynamics, Oxford University Press, 2013. ↩
- 48.T. Dauxois, Fermi, Pasta, Ulam and a mysterious lady, 2008, arXiv:0801.1590. ↩
- 49.M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G.S. Corrado, A. Davis, J. Dean, M. Devin, et al., Tensorflow: large-scale machine learning on heterogeneous distributed systems, 2016, arXiv:1603.04467. ↩
- 50.S.L. Brunton, J.L. Proctor, J.N. Kutz, Discovering governing equations from data by sparse identifification of nonlinear dynamical systems, Proc. Natl. Acad. Sci. 113 (2016) 3932–3937. ↩